どうも！初めましての方は初めまして、初心者のWebサイト勉強のとみーです！
待ち行列システムの中で、M/G/∞ 待ち行列の系内数はポアソン分布と密接な関係があります。
今回はその関係について詳しく見ていきましょう！
確率の基本的な知識がある方（高校数学〜大学入門）
M/G/∞ 待ち行列とは－ケンドールの記号の確認
まず、M/G/∞ 待ち行列とは何かを確認しておきましょう。
これはケンドールの記号を使った待ち行列の表現です。
ケンドールの記号について、詳しくは以下の記事で解説しています。
到着の確率分布/サービス時間の確率分布/サーバー数
というケンドールの記号の表記にしたがうと、M/G/∞ 待ち行列は
- M：到着の確率分布・確率過程
- G：サービス時間の確率分布
- ∞：サーバー数
となります。
到着の確率分布 M はマルコフ連鎖を表す
M はマルコフ連鎖を表しますが、ケンドールの記号では
を表します。
上の図では到着間隔 $X_{(\cdot)}$ に対して $X_{(\cdot)} \sim \mathcal{E} (\lambda)$ となります。
マルコフ連鎖が指数分布を表すのは、指数分布が連続型確率分布の中で唯一マルコフ性を持っているためです。
また、到着間隔の確率分布が指数分布なら確率過程はポアソン過程となるため、上のような組み合わせとなります。
サービスの確率分布 G は一般分布を表す
G は一般分布を表します。
つまり、特に指定がなくどの分布でもいいということです。
サーバー数が無限とはどういうことか
店舗のレジ待ちの場合、レジ（サーバー）が無限にあるということはありえないため、レジに列を作って並びます。
サーバーが無限にあるというのは、図書館のように並んで待たずに誰でも入れるようなシステムに対応します。
つまり、列を作らずにサービスを受けられる待ち行列です。
また、会員制のジムなど、収容人数は有限だけど全員が収容できる余裕があり、実質的に待ち時間なくサービスを利用できるシステムや、セルフサービスのシステムも「サーバー数∞」として考えられます。
M/G/∞ 待ち行列のまとめ
以上をまとめて M/G/∞ 待ち行列を整理すると、次のようになります。
M/G/∞ 待ち行列が理解できたら早速ポアソン分布との関係を見ていきましょう。
M/G/∞ 待ち行列の系内数はポアソン分布に従う
M/G/∞ 待ち行列には
系内数がポアソン分布に従う
という性質があります。
この性質について詳しく見ていきます。
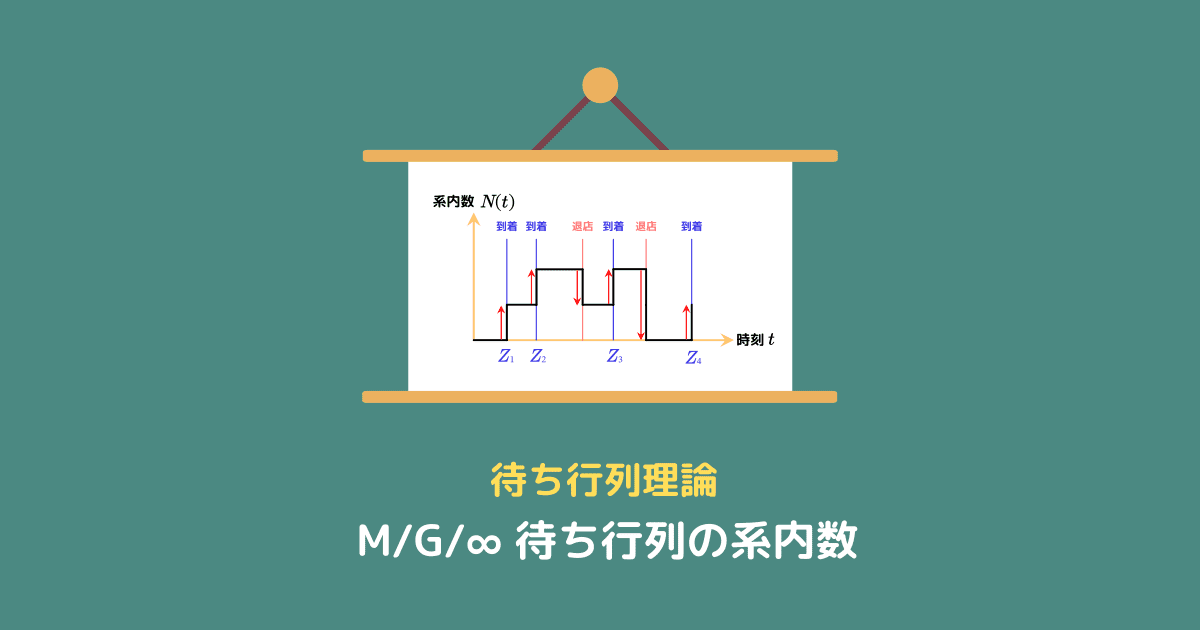
待ち行列の系内数とは
系内数はあまり聞き慣れない言葉ですが、待ち行列においては
（ある時刻に）システム内に留まっている人数
を意味します。
サーバー数が無限の状況では列に並んで待つ時間はないので、サービスを利用中の人数と言い換えることもできます。
図書館を例にすると、ある時刻において図書館内にいる人数が系内数ということになります。
会員制のジムの場合はトレーニング中の人数が系内数です。
M/G/∞ 待ち行列におけるポアソン分布
M/G/∞ 待ち行列では「到着の確率分布が指数分布」であることは上で説明した通りですが、そのほかに「到着の確率分布が指数分布なら到着数はポアソン過程（ポアソン分布）」という性質があります。
その性質と合わせれば、M/G/∞ 待ち行列において
- 到着数
- 系内数
の２つがポアソン分布に従うということになります。
また、時間がどれくらい経ったらポアソン分布に従うと見なして良いのでしょうか？
ここからは、この２つに焦点を当てて M/G/∞ 待ち行列について考えていきましょう。
確率や統計の専門性は理系の就活でかなり優位に働きます。
そのため、エンジニア就活特化のプラットフォームを使えば他では見られない高待遇な就職先が見つかります！
| 特徴 | リンク | |
|---|---|---|
| UZUZ理系 |
|
|
| エンジニア就活 |
|
|
| レバテックルーキー |
|
経験不足で大丈夫かな…という方はプログラミングスクールでスキルアップしておくとバッチリです。
| 特徴 | リンク | |
|---|---|---|
| エンジニアズゲート |
|
|
| TechAcademy |
|
エンジニアズゲート
M/G/∞ 待ち行列の系内数はなぜポアソン分布に従うのか
話をわかりやすくするために、ここでは客が来店しセルフサービス形式でサービスを利用する ATM を例に考えましょう。
ATM の台数は十分にあり、ATM 利用を開始するための待ち時間はないものとします。
重要な値を変数で表しましょう。
つまり、時刻 $t$ に ATM を利用している人が $N(t)$ 人です。
時刻 $x \in (0, t)$ に到着した客が時刻 $t$ で系内に留まっている確率
上の設定から時刻 $t$ までに $\Lambda (t)$ 人が到着しますが、ここで
時刻 $x \in (0, t)$ に到着した客が時刻 $t$ でも系内に留まっている確率
を考えましょう。
ここでの「系内」は「店内」の意味です。
上で確認したように、M/G/∞ 待ち行列ではサービス時間（系内に滞在する時間）は一般分布 $G$ に従います。
したがって、サービスが時間 $t$ 以内に終わる確率は $G(t)$ と表されます。
「時刻 $x \in (0, t)$ に到着した客が時刻 $t$ でも系内に留まっている」のは、サービス時間が $t \; – \; x$ 以上のときなので、その確率は
$$1 \; – \; G(t \; – \; x)$$
となります。
到着時刻の確率分布
ここで、$i$ 番目に到着した人の到着時刻を $Z_i$（$i \in [[1, n]]$） とします。
図にすると次のようになります。
詳しくはこちらの記事で丁寧に解説していますが、ポアソン過程の到着時刻には次のような性質があります。
$\Lambda(t) = n$ の場合、到着時刻 $(Z_1, Z_2, \cdots, Z_n)$ は
と同じ分布を持つ。
数式で表せば、$Z = (Z_1, \cdots, Z_n)$ として
$$\displaystyle f_Z (t_1, \cdots, t_n \;|\; \Lambda(t) = n) = \frac{n!}{t^n}$$
ということです。
$Z_1 \leq < \cdots < Z_n)$ なので、$t_1 \leq < \cdots < t_n)$ という制約があります。
$\Lambda (t) = n$ 人の客の到着時刻
$Z_i$ は $i$ 番目の到着時刻を表しますが、$\Lambda (t) = n$ 人の客の到着順は $n!$ 通り存在します。
よって、客 $j$ が時刻 $t_j$ に到着する確率は上の確率を $n!$ で割った
$$\displaystyle f_X (t_1, \cdots, t_n \;|\; \Lambda(t) = n) = \frac{1}{t^n}$$
となります。
客が時刻 $t$ に到着する確率
ある客 $j$ が時刻 $t$ に到着する確率は、上の確率を周辺化することで次のように求められます。
$$ \begin{align*} \mathbb{P} (X_j = t_j) &= \int f_X (t_1, \cdots, t_{j-1}, t_{j+1}, \cdots, t_n \;|\; \Lambda(t) = n) d X_1 \cdots dX_{j-1} d X_{j+1} \cdots dX_n \\ &= \int \frac{1}{t^n} d X_1 \cdots dX_{j-1} d X_{j+1} \cdots dX_n \\ &= \frac{1}{t^n} \int_0^t \cdots \int_0^t d X_1 \cdots dX_{j-1} d X_{j+1} \cdots dX_n \\ &= \frac{1}{t} \end{align*} $$
つまり、
客が時刻 $t$ に到着する確率は $\frac{1}{t}$
となります。
一様分布 $U_{[0, t]}$ ですね！
客が時刻 $t$ で系内に留まっている確率
以上のことから、ある客が時刻 $t$ で系内に留まっている確率 $p_t$ は次のようになります。
$$ \begin{align*} p_t &= \int_0^t \mathbb{P} (\text{時刻 } x \text{ に到着 かつ 時刻} t \text{ に留まっている}) dx \\ &= \int_0^t \mathbb{P} (\text{時刻 } t \text{ に留まっている} | \text{時刻 } x \text{ に到着}) \mathbb{P} (\text{時刻 } x \text{ に到着}) dx \\ &= \int_0^t \left (1 \; – \; G(t \; – \; x) \right) \frac{1}{t} dx \\ &= \frac{1}{t} \int_0^t \left (1 \; – \; G(t \; – \; x) \right) dx \end{align*} $$
分布によって $G$ は異なるのでこれ以上計算を進めることはできませんが、ここから $\Lambda (t)$ 人の客は
の２つに分かれることがわかります。
これは、ポアソン過程の到着をベルヌーイ試行で振り分けることに他なりません。
ポアソン過程の到着をベルヌーイ試行で振り分ける
詳しくはこちらの記事で解説していますが、到着率 $\lambda$ のポアソン過程 $\Lambda(t)$ を
のように２つのグループに分ける場合、グループ１、２の人数 $Y_1(t), Y_2(t) $ について
- $Y_1 (t), Y_2 (t)$ は互いに独立
- $Y_1 (t) \sim Pois(\lambda t p)$
- $Y_2 (t) \sim Pois(\lambda t q)$
が成り立ちます。
この性質を使うと、今回はポアソン過程を確率 $p_t, 1 \; – \; p_t$ で振り分けるので
となります。
したがって、系内数がポアソン分布に従うことが導かれました。
系内から去った人数もポアソン分布に従います！
M/G/∞ 待ち行列における系内数の極限分布
最後に $t$ が十分に大きくなった場合の系内数の分布を見てみましょう。
系内数が従うポアソン分布のパラメータの極限
系内数が従うポアソン分布のパラメータ $\lambda t p_t$ の極限は
$$ \begin{align*} \lim_{t \rightarrow \infty} \lambda t p_t = \lambda \lim_{t \rightarrow \infty} \int_0^t \left (1 \; – \; G(t \; – \; x) \right) du \end{align*} $$
で求められます。
積分については、確率密度関数 $g(u)$ とすると、次のように変形できます。
確率密度関数と累積分布関数の関係は $G(u) = \int_0^\infty g(u) du$ です。
$$ \begin{align*} \lim_{t \rightarrow \infty} \int_0^t \left (1 \; – \; G(t \; – \; x) \right) du &= \lim_{t \rightarrow \infty} \int_0^t \mathbb{P} (U \geq u) du \\ &= \lim_{t \rightarrow \infty} \int_0^t \int_u^\infty g(v) dv du \\ &= \lim_{t \rightarrow \infty} \int_u^\infty \int_0^t g(v) du dv \\ &= \lim_{t \rightarrow \infty} \int_u^\infty \int_0^t v g(v) dv \\ &= \mathbb{E} [U] \\ \end{align*} $$
$U$ はサービス時間を表す確率変数です。
待ち行列のサービス率
サービス時間の期待値の逆数
$$\mu = \frac{1}{\mathbb{E} [U]}$$
はサービス率と呼ばれます。
サービス率 $\mu$ を使うと、系内数が従うポアソン分布のパラメータ $\lambda t p_t$ の極限は
$$\lim_{t \rightarrow \infty} \lambda t p_t = \frac{\lambda}{\mu}$$
と表せます。
つまり、十分時間が経った状態の系内数はパラメータ $\frac{\lambda}{\mu}$ のポアソン分布に従います。
十分時間が経ったかどうかを判断する
「十分時間が経った」かどうかの判断を行う際は、
$G(t) \simeq 1$ となるような $t$ は十分に大きい
という事実が一つの基準となります。
$G(u)$ は累積分布関数なので単調増加であり、その値が $1$ に十分近いのであれば $t \geq u$ となる $t$ に対して積分の中身はほぼ $0$ となるからです。
このような $t$ を考える場合は $\int_0^t \left (1 \; – \; G(t \; – \; x) \right) du$ を計算することなく
$$N(t) \sim Pois(\frac{\lambda}{\mu})$$
として考えることができます。
まとめ
今回は、M/G/∞ 待ち行列の系内数についてご紹介しました。
系内数がポアソン分布でモデル化できるので、ここから色んな応用ができます！
コメント