【再生過程】均衡分布とは？待ち時間の極限分布を例に解説！

どうも！初めましての方は初めまして、初心者のWebサイト勉強のとみーです！

バス会社や鉄道会社のサービスを向上させるには、

乗客の待ち時間を減らす

ことが重要です。

しかし、運行本数や頻度を増やすのには限界がありますよね。

実は、運行本数や頻度を変えずに待ち時間を減らす方法は存在します。

そして、その方法を導くためには再生過程の均衡分布を理解する必要があります。

とみー

そこで今回は、バスの待ち時間を例に均衡分布と待ち時間を最小にする条件について解説していきます！

対象レベル

確率の基本的な知識がある方（高校数学〜大学入門）

関連する再生過程の記事

均衡分布とは？
待ち時間を考えるための再生過程
1. 問題の設定・条件
2. 待ち時間 $Y (t)$
待ち時間の分布を求めるための再生報酬過程
再生報酬定理
1. 部分報酬 ${R_{n}}$ の期待値 $E [R_{n}]$
2. 再生報酬定理の適用
待ち時間の分布－客の到着が一様分布
まとめ

均衡分布とは？

均衡分布とは、一言でいうと

待ち時間の極限分布

です。

とみー

といってもこれだけではわからないと思うので、詳しく説明します。

待ち時間を考えるための再生過程

均衡分布の話に入る前に、まずは問題の設定を明らかにしておきましょう。

問題の設定・条件

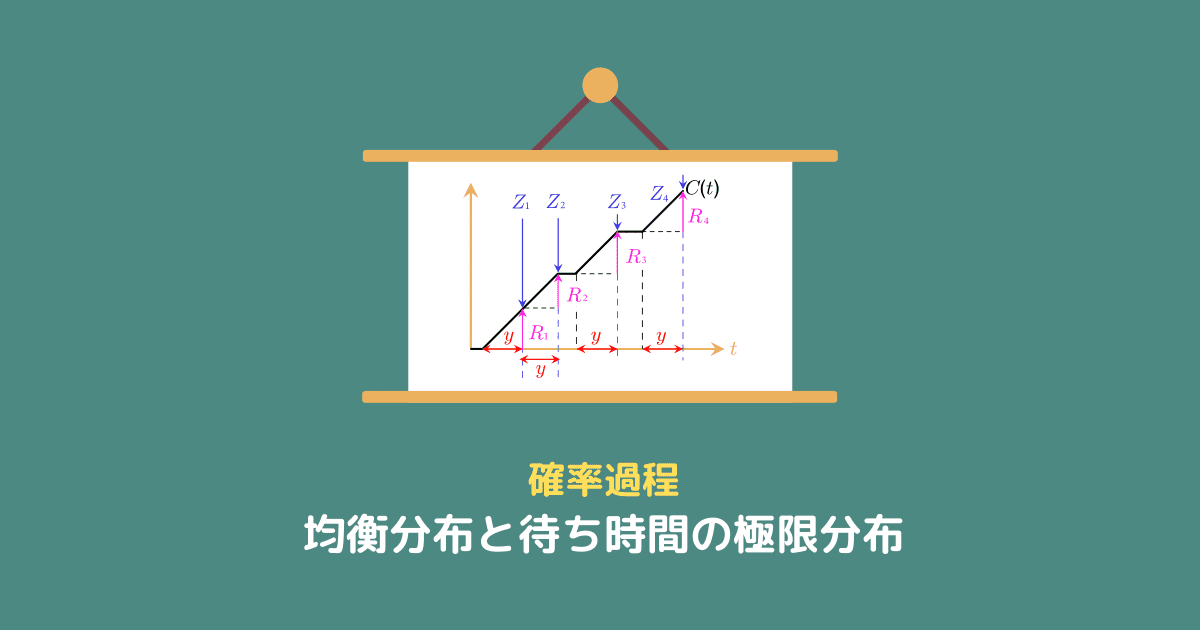
ここでは、バスの到着に関する再生過程を考えます。

次のように変数をおきましょう。

$X_{n}$ ： $n - 1$ 台目のバスと $n$ 台目のバスの到着間隔
$Z_{n}$ ： $n$ 台目のバスの到着時刻

図にすると、次の画像のような感じになります。

待ち時間 $Y (t)$

この再生過程で、時刻 $t$ に到着した客の待ち時間を $Y (t)$ とします。

再生過程 $M (t)$ は、時刻 $t$ までに到着したバスの本数を表します。

時刻 $t$ までに $M (t)$ 本到着するので、次のバスの到着時刻は $Z_{M (t) + 1}$ ですね。

とみー

この $Y (t)$ の確率分布がわかれば待ち時間の確率的な振る舞いがわかるので、最小化する方法が分かります。

そのため、 $Y (t)$ の確率分布

$F_{Y} (y) = P (Y (t) \leq y)$

（ $y$ は任意の定数）を求めることが目標になります。

しかし、これを求めるにはテクニックが必要なので、一旦次のような再生報酬過程を考えます。

待ち時間の分布を求めるための再生報酬過程

報酬の導入

求めたいのは

$P (Y (t) \leq y)$

なので、次のような報酬を考えます。

報酬

$\begin{array}{r} I_{{Y (t) \leq y}} (t) = {\begin{cases} 1 \dots Y (t) \leq y \\ 0 \dots Y (t) > y \end{cases} \end{array}$

これは、待ち時間が $y$ 以下となるような時刻 $t$ に客が到着できたら＋１の報酬がもらえることを表しています。

バスの到着ではないことに注意しましょう！

$X_{2} < y$ なので、区間 $X_{2}$ ではいつ到着しても報酬がもらえます。

とみー

言い方を変えると、バスの到着時刻の $y$ 分前に到着すれば＋１の報酬が発生します。

累積報酬 $C (t)$ （再生報酬過程）

報酬 $I_{{Y (t) \leq y}}$ の表現を使うと、再生報酬過程（累積報酬）は次のように表されます。

再生報酬過程

$C (t) = \int_{0}^{t} I_{{Y (u) \leq y}} (u) d u$

とみー

時刻 $t$ と紛らわしいので、積分変数は $u$ としています。

$Y (t) \leq y$ のとき報酬が１発生するので、累積報酬の傾きは１になります。

とみー

バスの到着時刻 ${Z_{n}}$ とは関係なく報酬が変化するので、これは部分報酬モデルです！

ちなみに、この $C (t)$ は $Y (t) \leq y$ となる時間の総和、つまり

時刻 $t$ までに $y$ 分以内でバスに乗れる時間がどれくらいあるか

を表しています。

時間の単位は問題によって秒・分・時間など様々です。

再生報酬関数 $c (t)$

再生報酬過程において、 $c (t) = E [C (t)]$ を再生報酬関数といいます。

今回の例では、

時刻 $t$ までに $y$ 分以内でバスに乗れる時間がどれくらいあると見込めるか

を表します。

$C (t) = \int_{0}^{t} I_{{Y (t) \leq y}} (t) d t$ を代入して計算を行うと

再生報酬関数

$c (t) = \int_{0}^{t} P (Y (u) \leq y) d u$

が得られます。

とみー

時刻 $t$ と紛らわしいので、ここでも積分変数は $u$ としています。

導出

$\begin{array}{rcl} c (t) & = & E [C (t)] \\ = & E [\int_{0}^{t} I_{{Y (u) \leq y}} (u) d u] \\ = & \int_{0}^{t} E [I_{{Y (u) \leq y}} (u)] d u \end{array}$

ここで、 $I_{{Y (u) \leq y}}$ は

$Y (u) \leq y$ のとき１
$Y (u) > y$ のとき０

なので、

$\begin{array}{rcl} E [I_{{Y (u) \leq y}} (u)] & = & 1 \cdot P (Y (u) \leq y) + 0 \cdot P (Y (u) > y) \\ = & P (Y (u) \leq y) \end{array}$

である。

よって

$c (t) = \int_{0}^{t} P (Y (u) \leq y) d u$

部分報酬 ${R_{n}}$

部分報酬モデルの考え方にしたがって、時刻 $Z_{n}$ の累積報酬と時刻 $Z_{n - 1}$ の累積報酬の差を部分報酬 $R_{n}$ とすると、

部分報酬

$\forall n \in N, R_{n} = m i n {X_{n}, y}$

となります。

再生報酬定理

ここまでで再生報酬過程が定義できたので、再生報酬定理を適用します。

再生報酬定理

すべての自然数 $n$ に対し、 $E [X_{n}] = \frac{1}{μ} < \infty, V [X_{n}] < \infty$ 、 $E [R_{n}] < \infty$ が成り立つとき、

$lim_{t \to \infty} \frac{c (t)}{t} = μ E [R_{n}]$

となる。

参考再生報酬定理については、こちらの記事で解説しています。

再生報酬定理とは？導出から解釈までわかりやすく解説

どうも！初めましての方は初めまして、初心者のWebサイト勉強のとみーです！再生過程には、再生過程と再生関数の極限に関する性質を示す基本再生定理（Elementary Renewal Theorem：ERT）という定理が存在します。参考 ...

とみー

途中の式変形で登場するので、部分報酬の期待値だけ最初に確認しておきましょう。

部分報酬 ${R_{n}}$ の期待値 $E [R_{n}]$

計算を行うと、 ${R_{n}}$ の期待値は

$E [R_{n}] = \int_{0}^{y} P (X_{n} > x) d x$

であることが求められます。

導出

部分積分を使うと

$\begin{array}{rcl} \int_{0}^{\infty} P (R_{n} > x) d x & = & {[x P (R_{n} > x)]}_{0}^{\infty} - \int_{0}^{\infty} x \frac{\partial}{\partial x} P (R_{n} > x) d x \\ = & 0 - \int_{0}^{\infty} x \frac{\partial}{\partial x} (1 - P (R_{n} \leq x)) d x \\ = & - \int_{0}^{\infty} x \frac{\partial}{\partial x} (1 - F_{R} (x)) d x \\ = & - \int_{0}^{\infty} x (- f_{R} (x)) d x \\ = & \int_{0}^{\infty} x f_{R} (x) d x \\ = & E [R_{n}] \end{array}$

となる。

ここで、

$\begin{array}{rcl} \int_{0}^{\infty} P (R_{n} > x) d x & = & \int_{0}^{y} P (R_{n} > x) d x + \int_{y}^{\infty} P (R_{n} > x) d x \end{array}$

だが、 $R_{n} \leq y$ なので $y < x$ のとき

$R_{n} > x$

となることはない。よって、

$\int_{y}^{\infty} P (R_{n} > x) d x = 0$

また、 $x < y$ のとき

$\begin{array}{rcl} R_{n} > x & ⟺ & m i n {X_{n}, y} > x \\ ⟺ & X_{n} > x \end{array}$

なので

$\int_{0}^{\infty} P (R_{n} > x) d x = \int_{0}^{\infty} P (X_{n} > x) d x$

以上をまとめると

$E [R_{n}] = \int_{0}^{y} E (X_{n} > x) d x$

再生報酬定理の適用

上で求めた $c (t)$ の表現を使うと、

$\frac{c (t)}{t} = \frac{1}{t} \int_{0}^{t} P (Y (u) \leq y) d u$

なので、再生報酬定理を適用すると

$lim_{t \to \infty} \frac{1}{t} \int_{0}^{t} P (Y (u) \leq y) d u = μ \int_{0}^{y} P (X_{n} > x) d x$

となります。

とみー

これは後で式変形のために使うので、どういう意味かは置いておきましょう。

待ち時間の分布－客の到着が一様分布

さて、ここまでの話は客の到着時間に関して何も仮定していませんでした。

とみー

要するに、到着時間がどんな確率分布にしたがっていても成り立ちます。

ここからは、話をさらに深めていくために客が時刻 $0$ から $t$ の間でランダムに到着するとしましょう。

つまり、客の到着時間を $U$ としたときに、

$U$ は一様分布 $U_{[0, t]}$ にしたがう

と仮定します。

このとき、確率密度関数は

$\begin{array}{r} f_{U} (u) = {\begin{cases} \frac{1}{t} \dots u \in [0, t] \\ 0 \dots u \notin [0, t] \end{cases} \end{array}$

です。

待ち時間の確率分布

客の到着時間が一様分布にしたがうとき、待ち時間の累積分布関数は

$P (Y (U) \leq y) = \int_{0}^{\infty} P (Y (u) \leq y) f_{U} (u) d u$

です。

とみー

これは累積分布関数を確率密度関数で表しただけです。

確率密度関数 $f_{U}$ を代入すると

$P (Y (U) \leq y) = \frac{1}{t} \int_{0}^{t} P (Y (u) \leq y) d u$

となります。

とみー

これは先ほど上で見た $\frac{c (t)}{t}$ に他なりません！

待ち時間の極限分布と均衡分布

$P (Y (U) \leq y)$ と $\frac{c (t)}{t}$ が同じということは、先ほどの再生報酬定理の結果が使えるので

$lim_{t \to \infty} P (Y (U) \leq y) = μ \int_{0}^{y} P (X_{n} > x) d x$

が成り立ちます。

とみー

これが待ち時間の極限分布です！

そして、この式の右辺は

$μ \int_{0}^{y} P (X_{n} > x) d x = μ \int_{0}^{y} (1 - F_{X} (x)) d x$

と書き直すことができます。

これは $y$ についての関数と見ることができるので、ここで

$F_{e} (y) = μ \int_{0}^{y} (1 - F_{X} (x)) d x$

としましょう。

すると、 $F_{e} (y)$ は

$y$ についての累積分布関数

になっています。

確認

$F_{e}$ が累積分布関数であることを示すためには、

非減少
$lim_{y \to \infty} F_{e} (y) = 1$

の２つを確かめればOKです。

まず、 $y_{1} < y_{2}$ とすると、

$\begin{array}{rcl} F_{e} (y_{2}) - F_{e} (y_{1}) & = & μ \int_{0}^{y_{2}} (1 - F_{X} (x)) d x - μ \int_{0}^{y_{1}} (1 - F_{X} (x)) d x \\ = & \int_{0}^{y_{1}} (1 - F_{X} (x)) d x + \int_{y_{1}}^{y_{2}} (1 - F_{X} (x)) d x - μ \int_{0}^{y_{1}} (1 - F_{X} (x)) d x \\ = & \int_{y_{1}}^{y_{2}} (1 - F_{X} (x)) d x \end{array}$

$F_{X}$ は確率変数 ${X_{n}}$ の累積分布関数だから

$1 - F_{X} (x) \geq 0$

よって、 $F_{e} (y_{2}) > F_{e} (y_{1})$ だから $F_{e}$ は非減少。

また、

$\begin{array}{rcl} μ \int_{0}^{\infty} (1 - F_{X} (x)) d x & = & \frac{1}{E [X]} \cdot E [X] \\ = & 1 \end{array}$

なので、 $lim_{y \to \infty} F_{e} (y) = 1$ 。

この $F_{e}$ を確率分布関数 $F_{X}$ の均衡分布（の生存関数）といいます。

均衡分布の生存関数

$F_{e} (y) = μ \int_{0}^{y} (1 - F_{X} (x)) d x$

均衡分布の確率密度関数は、

$f_{e} (y) = μ (1 - F_{X} (x))$

です。

待ち時間の期待値

以上で待ち時間の極限分布がわかったので、最後に期待値を求めると

待ち時間の期待値

$E [Y] = \frac{1}{2} μ (V [X_{n}] + \frac{1}{μ^{2}})$

となります。

導出

まず、計算に必要なので次の式変形を考える。

$\begin{array}{rcl} E [X^{2}] & = & \int_{0}^{\infty} P (X^{2} > x) d x \\ = & \int_{0}^{\infty} P (X > x^{\frac{1}{2}}) d x \end{array}$

$x = y^{2}$ という変数変換をすると、 $d x = 2 y d y$ なので

$\begin{array}{rcl} E [X^{2}] & = & 2 \int_{0}^{\infty} y P (X > y) d y \\ = & 2 \int_{0}^{\infty} y (1 - F_{X} (y)) d y \end{array}$

となる。

よって、

$\int_{0}^{\infty} y (1 - F_{X} (y)) d y = \frac{1}{2} E [X_{n}^{2}]$

これを用いると、

$\begin{array}{rcl} E [Y] & = & \int_{0}^{\infty} y f_{e} (y) d y \\ = & μ \int_{0}^{\infty} y (1 - F_{X} (y)) d y \\ = & \frac{1}{2} μ E [X_{n}^{2}] \\ = & \frac{1}{2} μ (V [X_{n}] + E [X_{n}]^{2}) \\ = & \frac{1}{2} μ (V [X_{n}] + \frac{1}{μ^{2}}) \end{array}$