どうも!初めましての方は初めまして、初心者のWebサイト勉強のとみーです!
ここ数年の機械学習・人工知能に対する需要・人気の高まりを受けて、背景となる統計・数学について勉強する機会も増えてきました。
最近ではプログラミング言語が非常に使いやすくなっており、たったの数行で機械学習ができるようになってきています!
統計学を勉強する上での第一歩は、データをどのように表記するかを理解することです。

そこで今回は、データを表すために使われる記号の使い方について見ていきましょう!
確率の基本的な知識がある方(高校数学〜大学入門)
統計学におけるデータの表記法
データの書き方には色々なバリエーションがありますが、本サイトでは
の3つをデータを表す文字として使います。

それぞれの使い方は、例を通して見ていきましょう。
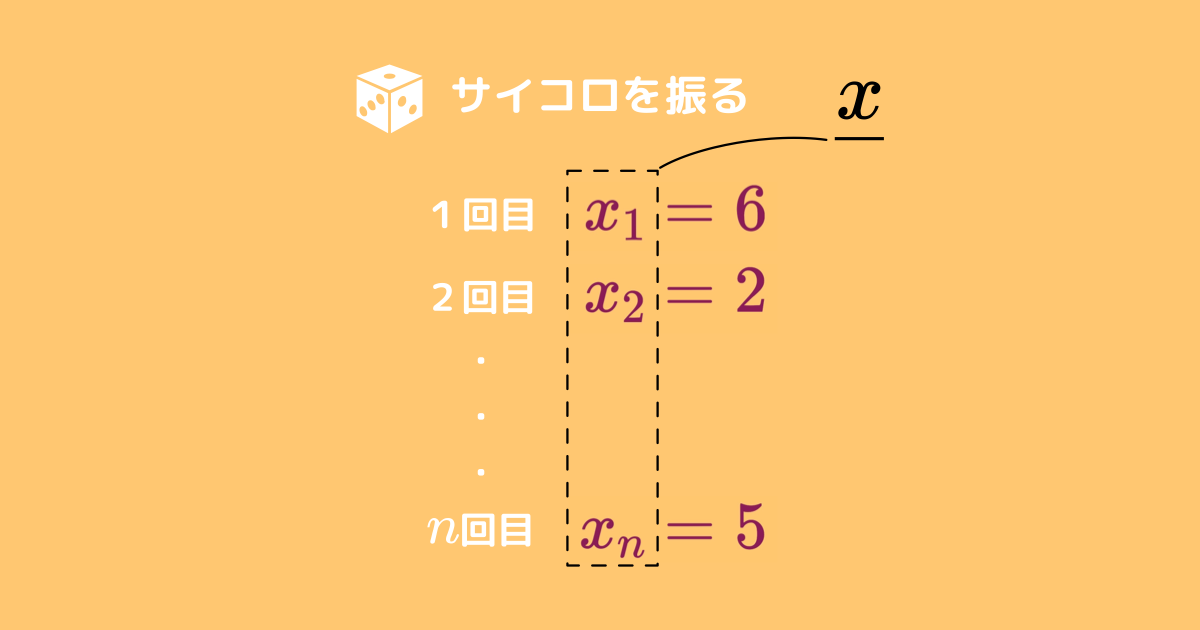
サイコロを
のように表すことにします。
この表記を用いると、サイコロを7回振った結果は次の表のようになります。
| 3 | 5 | 1 | 2 | 2 | 6 | 3 |
1回目に3が出て、2回目に5が出て、…といった感じですね。
このとき、集められたデータをわざわざ
としてベクトルのように表します。
先ほどの表のデータは、
が成り立ちます。

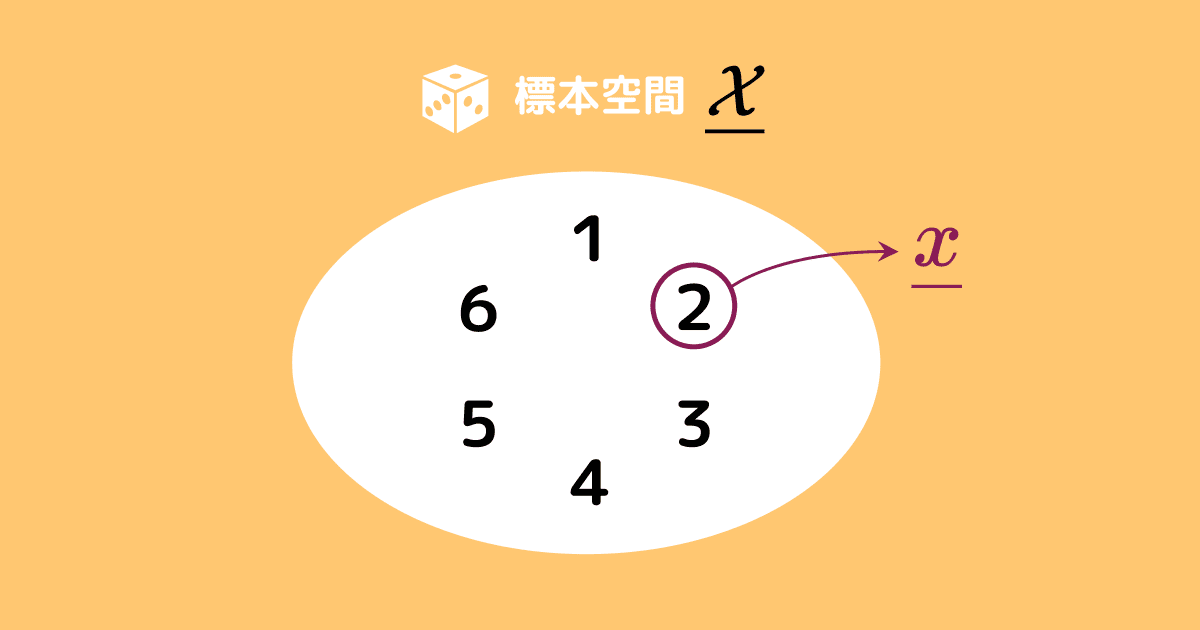
1〜6の中から1つを選ぶイメージですね。
このとき、上の式の
このように、すべての場合を含んだ集合を標本空間(母集団)と呼び、
先ほどの
となります。これは、標本は母集団から集められると言う意味です(当然ですね)。
例えばサイコロを2回振った場合、
となります。
同様に
が成り立ちます。
先ほど

つまり、
このようにどっちつかずの状態だと扱いが難しいので、次のように考えます。
- (サイコロを振る前)サイコロを1回振る時に出る目を
- まだサイコロを振っていないので、
- (サイコロを振った後)目が出たので
ポイントは、実際に出る前の目を大文字
このように、起こりうる値(今回の例だとサイコロの目)を変数として考えた
確率変数は、確率分布に従います。
例えばサイコロはどの目も
1回目に出た目(実現値)が
まとめて考えると、実現値が
練習問題
問題1
コインを3回投げ、順番に表、裏、裏の結果が得られました。このときの
ちなみに、
問題2
コインを2回投げた時の目を
まとめ
今回は、統計学を学ぶ上での第一歩となるデータの表記法についてご紹介しました。

これらの表記を使って、統計学の勉強をスタートしましょう!




コメント