どうも！初めましての方は初めまして、初心者のWebサイト勉強のとみーです！
ポアソン過程は、
ある時刻までに希少現象が発生した回数の総和
をモデル化できる確率過程で、待ち行列理論でよく用いられます。
参考 ポアソン過程の基礎については、こちらでわかりやすくまとめています。
ポアソン過程には、重要な性質がいくつかあります。
そして、ポアソン過程を扱う問題では、
ポアソン過程のイベントをランダムに２分割する
設定がしばしば登場します。
今回は、そのような設定でよく利用する定理を証明付きでわかりやすくまとめました！
確率の基本的な知識がある方（高校数学〜大学入門）
ポアソン過程のイベントをベルヌーイ試行で間引くとは
まず、話をわかりやすくするために設定を明らかにしておきましょう。
到着率 $\lambda$ のポアソン過程
今回は、ポアソン過程として時刻 $t$ までに店に到着した客数 $\Lambda(t)$ を考えます。
ここでは客数としましたが、バスの到着や電話の着信など、ポアソン過程でモデル化できるものなら何でも構いません。
また、ポアソン過程の到着率を $\lambda$ とします。つまり、
$\Lambda (t) \sim Pois(\lambda t)$
です。
$i$ 番目の客の到着時刻を $Z_i$ とすると、次の図のようになります。
そして、このポアソン過程をベルヌーイ試行で間引くことを考えます。
ベルヌーイ試行による間引き
ベルヌーイ試行とは、
- 取り得る結果が２通り
- どちらが発生する確率も一定
という試行です。
例えばコイントスは結果が「表」と「裏」の２通りだけで、表が出る確率、裏が出る確率はともに常に $\frac{1}{2}$ のベルヌーイ試行です。
そのほかにも
- サイコロの目が３の倍数かどうか
- ５４枚のトランプの山から１枚引いた時に、それがジョーカーかどうか
といった試行もベルヌーイ試行となります。
確率が一定というのは、外的要因によらず何回試行を繰り返しても一定であることを意味します。
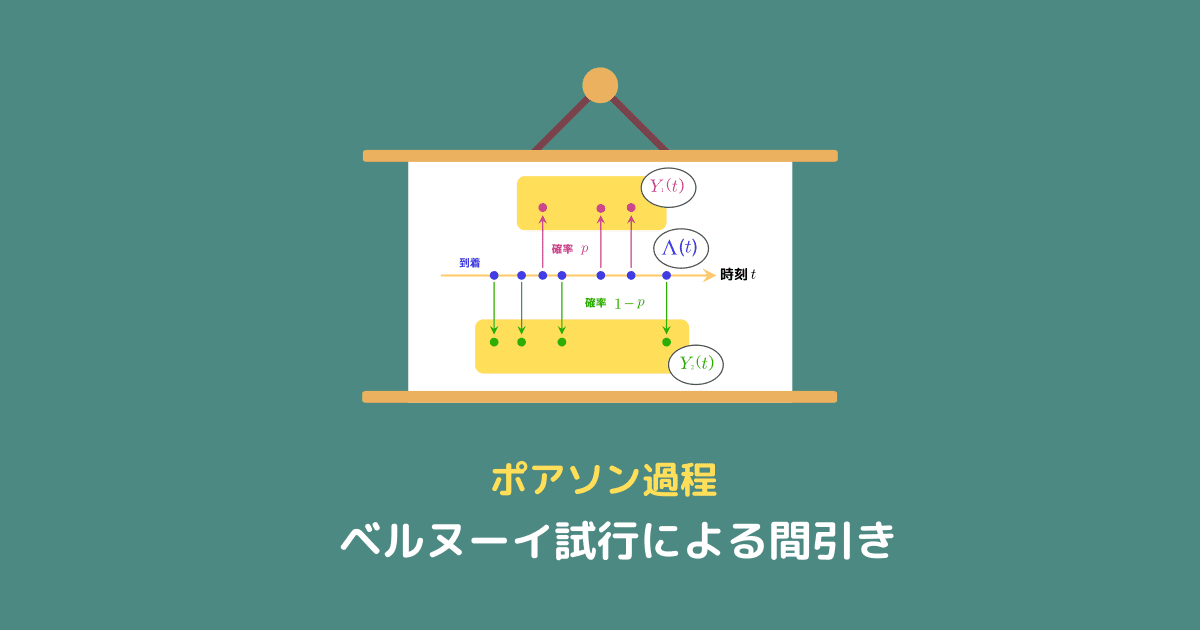
ベルヌーイ試行によるポアソン過程のイベントの間引き
ベルヌーイ試行が理解できたら、もとの問題の設定に戻りましょう。
今回は、時刻 $t$ までに到着した $\Lambda(t)$ 人の客のそれぞれを
というルールによってグループ分けすることを考えます。
つまり、パラメータ $p, q \;(= 1 \;-\; p)$ による $\Lambda(t)$ 回のベルヌーイ試行となります。
グループ１、グループ２という名前だと抽象的で理解しにくいですが、具体例として
のようなものが該当します。
当然この形にはまっていれば店内にいる人・退店した人というグループ分け以外でも適用できるため、かなり応用範囲が広い設定です。
ポアソン過程をベルヌーイ試行で間引くとポアソン過程になる
このようにしてポアソン過程を分割し、次のようになったとします。
するとこのとき、次の定理が成り立ちます。
- $Y_1 (t), Y_2 (t)$ は互いに独立
- $Y_1 (t) \sim Pois(\lambda t p)$
- $Y_2 (t) \sim Pois(\lambda t q)$
２と３は、元のポアソン分布のパラメータに、ベルヌーイ試行の対応する確率をかけたパラメータを持つポアソン分布になることを表しています。
定理をわかりやすく言い換える
この定理を簡単にいえば、
ポアソン過程をベルヌーイ試行で間引いたものは、ポアソン過程になる
ということになります。
この定理を単体で使うというよりは、他の問題を解く最中に使うことが多いです。
導出にあたって必要な知識を整理しておきましょう。
確率や統計の専門性は理系の就活でかなり優位に働きます。
そのため、エンジニア就活特化のプラットフォームを使えば他では見られない高待遇な就職先が見つかります！
| 特徴 | リンク | |
|---|---|---|
| UZUZ理系 |
|
|
| エンジニア就活 |
|
|
| レバテックルーキー |
|
経験不足で大丈夫かな…という方はプログラミングスクールでスキルアップしておくとバッチリです。
| 特徴 | リンク | |
|---|---|---|
| エンジニアズゲート |
|
|
| TechAcademy |
|
エンジニアズゲート
ベルヌーイ試行と二項分布
先ほど説明した通り、ベルヌーイ試行は「成功・失敗」のように２つの結果のうちのどちらかとなる試行です。
ベルヌーイ試行を $n$ 回繰り返したときに $k$ 回成功する確率は二項分布 $B(n, k)$ として知られており、確率質量関数は次のように表されます。
$_n C_k \; p^k \; (1 \;-\; p)^{(1 \;-\; k)}$
「成功する確率」という書き方をしましたが、問題設定に応じて「３の倍数が出る確率」といった具合に適宜読み替えて大丈夫です。
ポアソン分布の確率質量関数
こちらは復習になりますが、到着率 $\lambda$ の場合ポアソン分布のパラメータは $\lambda t$ なので、ポアソン分布の確率質量関数は以下の通りです。
$P(\Lambda (t) = k) = \displaystyle \frac{(\lambda t)^k e^{-\lambda t}}{k!}$
以上の知識で導出に取り掛かれます！
導出
$ \begin{eqnarray} P (Y_1 (t) = i, Y_2 (t) = j) &=& \color{blue} P (Y_1 (t) = i, Y_2 (t) = j | \Lambda (t) = i+j) \color{black} \; P (\Lambda (t) = i+j) \\ &=& \color{blue} P (Y_1 (t) = i | \Lambda (t) = i+j) \color{black} \; P (\Lambda (t) = i+j) \\ &=& \color{blue} {}_{i+j} C_i \; p^i \; q^j \color{black} \; \frac{(\lambda t)^{(i + j)} e^{-\lambda t}}{(i + j)!} \\ &=& \color{blue} \frac{(i + j)!}{i!j!} \; p^i \; q^j \color{black} \; \frac{(\lambda t)^{(i + j)} e^{-\lambda t}}{(i + j)!} \\ &=& \frac{(\lambda t p)^i }{i!} \frac{(\lambda t q)^j }{j!} \color{red} e^{-\lambda t}\color{black} \\ &=& \frac{(\lambda t p)^i \color{red} e^{-\lambda t p} \color{black} }{i!} \frac{(\lambda t q)^j \color{red} e^{-\lambda t q} \color{black} }{j!} \\ \end{eqnarray} $
最後の２行は $p + q = 1$ であることを使って $e^{-\lambda t} = e^{-\lambda t (p + q)}$ として変形しています。
周辺化を行って同様の変形を行うと次のようになります。
$ \begin{eqnarray} P (Y_1 (t) = i) &=& \sum_{j = 0}^\infty P (Y_1 (t) = i | \Lambda (t) = i+j) \; P (\Lambda (t) = i+j) \\ &=& \frac{(\lambda t p)^i e^{-\lambda t p}}{i!} \color{red} \sum_{j = 0}^\infty \color{black} \frac{\color{red} (\lambda t q)^j \color{black} e^{-\lambda t q} }{\color{red} j!} \\ &=& \frac{(\lambda t p)^i e^{-\lambda t p}}{i!} \color{red} e^{\lambda t q} \color{black} e^{-\lambda t q}\\ &=& \frac{(\lambda t p)^i e^{-\lambda t p}}{i!} \end{eqnarray} $
赤字の部分はネイピア数のマクローリン展開です。
これを $P (Y_2 (t) = j)$ に対して行うと
$ \begin{eqnarray} P (Y_2 (t) = j) &=& \frac{(\lambda t q)^i e^{-\lambda t q}}{i!} \end{eqnarray} $
ここで、$P (Y_1 (t) = i)$ と $P(Y_2 (t) = j)$ をよく見ると、
となっています。
つまり、
であることが示されました。
さらに最初の式に戻ると、最終行は「$i を含む値 \times j を含む値$」なので、
$$ \begin{eqnarray} P (Y_1 (t) = i, Y_2 (t) = j) &= \frac{(\lambda t p)^i e^{-\lambda t p} }{i!} \frac{(\lambda t q)^j e^{-\lambda t q} }{j!} \\ &= P (Y_1 (t) = i) P(Y_2 (t) = j) \end{eqnarray} $$
となっていることがわかります。
これで $Y_1(t)$ と $Y_2 (t)$ が独立であることが示されました。
以上で定理が示されました。
- $Y_1 (t), Y_2 (t)$ は互いに独立
- $Y_1 (t) \sim Pois(\lambda t p)$
- $Y_2 (t) \sim Pois(\lambda t q)$
まとめ
今回は、ポアソン過程をベルヌーイ試行で間引くとポアソン過程になる定理を証明しました。
この定理を念頭に置いておくと解ける問題の幅が広がります！
コメント