どうも!初めましての方は初めまして、初心者のWebサイト勉強のとみーです!
再生過程には、再生過程と再生関数の極限に関する性質を示す基本再生定理(Elementary Renewal Theorem:ERT)という定理が存在します。
参考 再生過程の基礎については、こちらの記事をご覧ください。
参考 基本再生定理については、こちらの記事をご覧ください。
そして、再生過程を拡張した再生報酬過程にも似たような再生報酬定理(Renewal Reward Theorem:RRT)という定理があります。

そこで今回は、その再生報酬定理について解説します!
確率の基本的な知識がある方(高校数学〜大学入門)
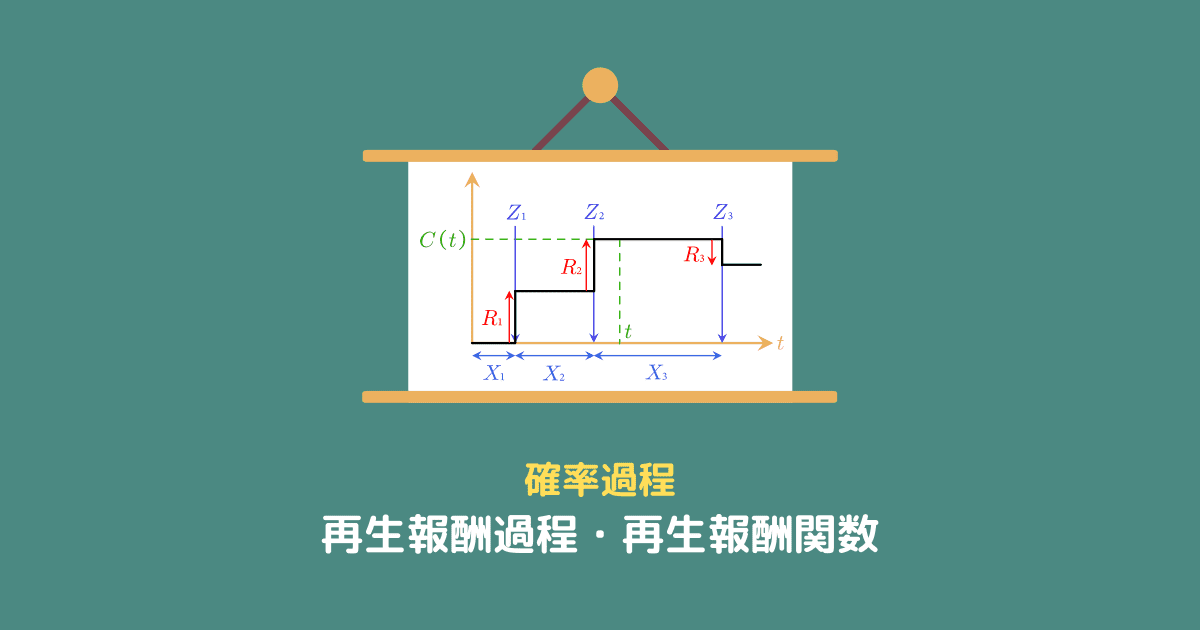
イメージをしやすくするために、電車の駅に到着した客が購入する切符による売上を題材として
という風に変数を置きます。
図にすると、次のような感じです。
参考 再生報酬過程の基本や切符の売上の例の詳しい説明は、こちらの記事をご覧ください。
再生報酬定理(RRT)とは
再生報酬定理の導出・理解のために必要な
確率変数の概収束
についてはじめに押さえましょう。
確率変数の概収束(ほとんど確実に収束)

基本再生定理のときと同じなので、概収束が何かわかっている人はスキップしてOKです!
再生報酬定理は概収束を使った定理なので、概収束のイメージを掴んでおきましょう。
確率変数列 $\{X_n\}_{n \in \mathbb{N}}$ と確率変数 $X$ が
$$\mathbb{P} \left( \lim_{n \to \infty} X_n = X \right) = 1$$
を満たすとき、$\{X_n\}$ は $X$ に概収束(ほとんど確実に収束)するといい、
$$X_n \xrightarrow[n \to \infty]{a.s.} X$$
と表す。

概収束は、収束する確率が1という意味です。
再生報酬定理
再生報酬定理とは、再生報酬過程・再生報酬関数の極限に関する次の関係のことです。
すべての自然数 $n$ に対し、$\mathbb{E}[X_n] = \frac{1}{\mu} < \infty, \mathbb{V}[X_n] < \infty$、$\mathbb{E}[R_n] < \infty$ が成り立つとき、
- $\displaystyle \frac{C(t)}{t} \xrightarrow[t \to \infty]{a.s.} \mu \mathbb{E}[R_n]$
- $\displaystyle \lim_{t \to \infty} \frac{c(t)}{t} = \mu \mathbb{E}[R_n]$
となる。
証明は結構複雑なので後回しにしましょう。

基本再生定理と同様に式の形と直感的な意味が理解できれば十分です。
再生報酬定理の直感的なイメージ
定理に登場する
- $\frac{C(t)}{t}$
- $\frac{c(t)}{t}$
の意味をまず整理しましょう。
$\frac{C(t)}{t}$
$C(t)$ は、時刻 $t$ までの累積報酬(総売上)を表しています。
その $C(t)$ を時間 $t$ で割っているので、$\frac{C(t)}{t}$ は総売上の時間平均です。つまり、
単位時間あたりの報酬
を表しています。
単位時間とは、1秒や1分など時間を測る際の基準となる時間です。
$\displaystyle \frac{C(t)}{t} \xrightarrow[t \to \infty]{a.s.} \mu \mathbb{E}[R_n]$
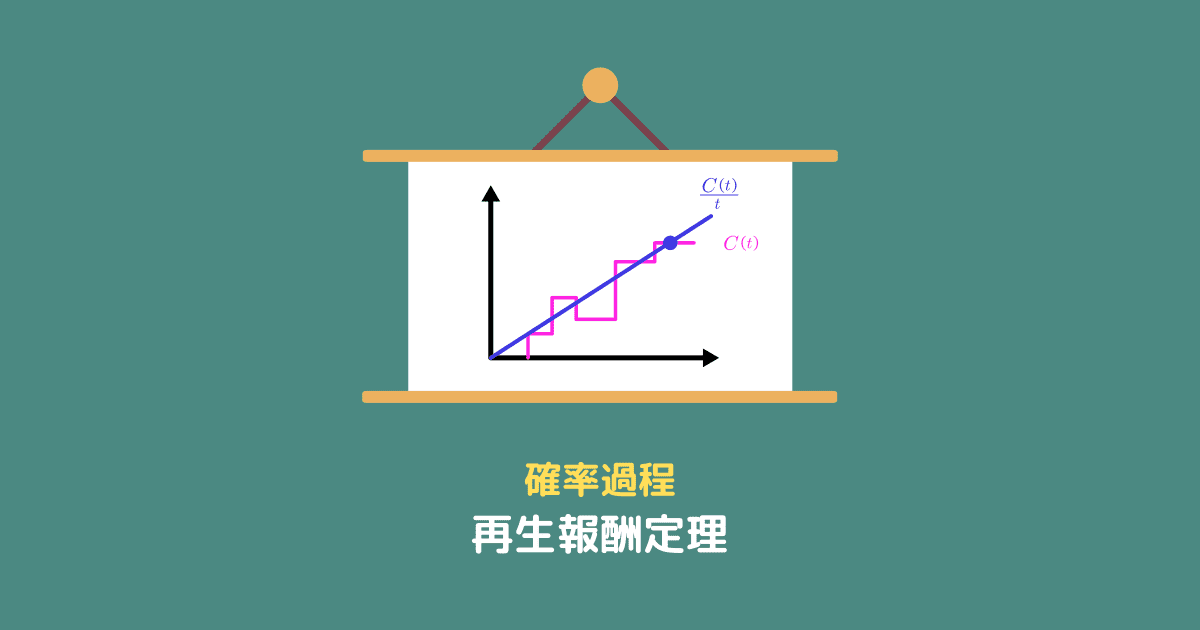
$\frac{C(t)}{t}$ が単位時間あたりの到着数なので、時間に関する極限を取った $\frac{C(t)}{t} \xrightarrow[t \to \infty]{a.s.}$ は、
十分長い時間が経った時の単位時間あたりの報酬
を表しています。
下の画像を見るとイメージがつかみやすいと思います。
$\mu$ と $\mathbb{E}[R_n]$ はそれぞれ次のような意味です。
1回の到着で $\mathbb{E}[R_n]$ だけ報酬がもらえて、単位時間に $\mu$ 回到着がある見込みなので、単位時間でもらえる報酬は直感的に $\mu \mathbb{E}[R_n]$ となりそうですよね。
再生報酬過程の
$$\displaystyle \frac{C(t)}{t} \xrightarrow[t \to \infty]{a.s.} \mu \mathbb{E}[R_n]$$
は、十分に時間が経てば確かに単位時間あたりの報酬は $\mu \mathbb{E}[R_n]$ になるということを示しています。

つまり、基本再生定理と同様に直感通りの結果になるというのが再生報酬定理①の主張です。
続いて、$\frac{c(t)}{t}$ についてです。
$\frac{c(t)}{t}$
$c(t) = \mathbb{E}[C(t)]$ なので、$c(t)$ は時刻 $t$ の時点でどれくらい報酬が出ていることが見込まれるかを表しています。
その $c(t)$ を時間 $t$ で割った $\frac{c(t)}{t}$ は、
単位時間あたりに見込まれる報酬
を表しています。

$\frac{C(t)}{t}$ と $\frac{c(t)}{t}$ の違いは、実際に計測した報酬額か見込まれる報酬額かです。
$\displaystyle \lim_{t \to \infty} \frac{c(t)}{t} = \mu \mathbb{E}[R_n]$
$\frac{c(t)}{t}$ が単位時間あたりに見込まれる報酬を表すので、時間に関する極限を取った $\lim_{t \to \infty} \frac{c(t)}{t}$ は
十分長い時間が経った時の単位時間あたりの見込み報酬
を表しています。
これが $\mu \mathbb{E}[R_n]$ に収束するので、
$$\frac{C(t)}{t} \xrightarrow[t \to \infty]{a.s.} \lim_{t \to \infty} \frac{c(t)}{t}$$
が成り立ちます。
これは、十分に長い時間が経つと
が一致することを表しています。

つまり、「見込み」と「実際」が一致するというのがこの定理の主張です!
再生報酬定理のイメージはつかめたでしょうか?
以上で説明は終了です。ここからは証明になるので、興味がある方はじっくり読んでみましょう。
再生報酬定理①の証明
再生報酬定理①
$$\displaystyle \frac{C(t)}{t} \xrightarrow[t \to \infty]{a.s.} \mu \mathbb{E}[R_n]$$
の証明は、大数の強法則と基本再生定理を使うと簡単に行えます。
大数の強法則
独立同分布の確率変数列 $\{X_n\}_{n \in \mathbb{Z}+}$ について、
が成り立つとき、
$$\frac{1}{n} \sum_{i=1}^n X_i \xrightarrow[n \to \infty]{a.s.} \mu$$
が成り立つ。
基本再生定理
2以上のすべての整数 $n$ に対し、$\mathbb{E} [X_n]= \frac{1}{\mu} < \infty, \mathbb{V}[X_i] < \infty$ が成り立つとき、
$$\displaystyle \frac{M(t)}{t} \xrightarrow[t \to \infty]{a.s.} \mu$$
となる。
詳しくは、「基本再生定理とは?導出から解釈までわかりやすく解説」の記事で解説しています。
証明
\begin{eqnarray} \frac{C(t)}{t} &=& \frac{\sum_{i=1}^{M(t)} R_i}{t} \\ &=& \frac{\sum_{i=1}^{M(t)} R_i}{M(t)} \frac{M(t)}{t} \end{eqnarray}
$M(t) \xrightarrow[t \to \infty]{a.s.} \infty$ なので、大数の強法則より
$$\frac{\sum_{i=1}^{M(t)} R_i}{M(t)} \xrightarrow[t \to \infty]{a.s.} \mathbb{E}[R_n]$$
が成り立つ。
また、基本再生定理より
$$\frac{M(t)}{t} \xrightarrow[t \to \infty]{a.s.} \mu$$
よって、
\begin{eqnarray} \frac{C(t)}{t} &=& \frac{\sum_{i=1}^{M(t)} R_i}{M(t)} \frac{M(t)}{t} \\ &\xrightarrow[t \to \infty]{a.s.}& \mathbb{E}[R_n] \mu \end{eqnarray}
基本報酬定理②の証明
再生報酬定理②
$$\displaystyle \lim_{t \to \infty} \frac{c(t)}{t} = \mu \mathbb{E}[R_n]$$
の証明は、基本再生定理を使えば簡単です。
証明
\begin{eqnarray} \frac{c(t)}{t} &=& \frac{\mathbb{E}[C(t)]}{t} \\ &=& \frac{\mathbb{E}[C(t)]}{M(t)} \frac{M(t)}{t} \end{eqnarray}
まず、定理①のときと同様に基本再生定理から
$$\frac{M(t)}{t} \xrightarrow[t \to \infty]{a.s.} \mu$$
が成り立つ。
また、
\begin{eqnarray} \frac{\mathbb{E}[C(t)]}{M(t)} &=& \frac{\mathbb{E} \left[\sum_{i=1}^{M(t)} R_i \right]}{M(t)} \\ &=& \frac{M(t) \mathbb{E}[R_n]}{M(t)} \\ &=& \mathbb{E}[R_n] \end{eqnarray}
であるから、
\begin{eqnarray} \frac{c(t)}{t} &=& \frac{\mathbb{E}[C(t)]}{t} \\ &=& \frac{\mathbb{E}[C(t)]}{M(t)} \frac{M(t)}{t} \\ &\xrightarrow[t \to \infty]{}& \mathbb{E}[R_n] \mu \end{eqnarray}

コメント